Proper CFL Number for Breaking Wave Force on Wall

barrybarry
in DualSPHysics v5.0

Hi all, I am trying to model a wave-structure interaction problem with DualSPHysics.

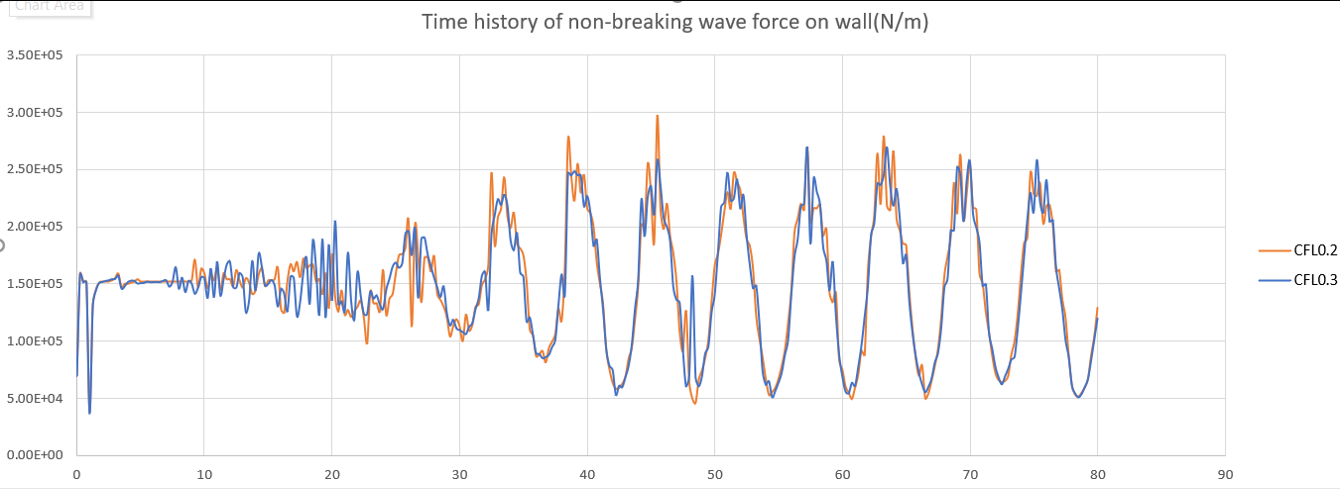
For non-breaking wave cases, since there isn't much "impulsive" behavior, the result isn't sensitive to the CFL number.

Picture2.png

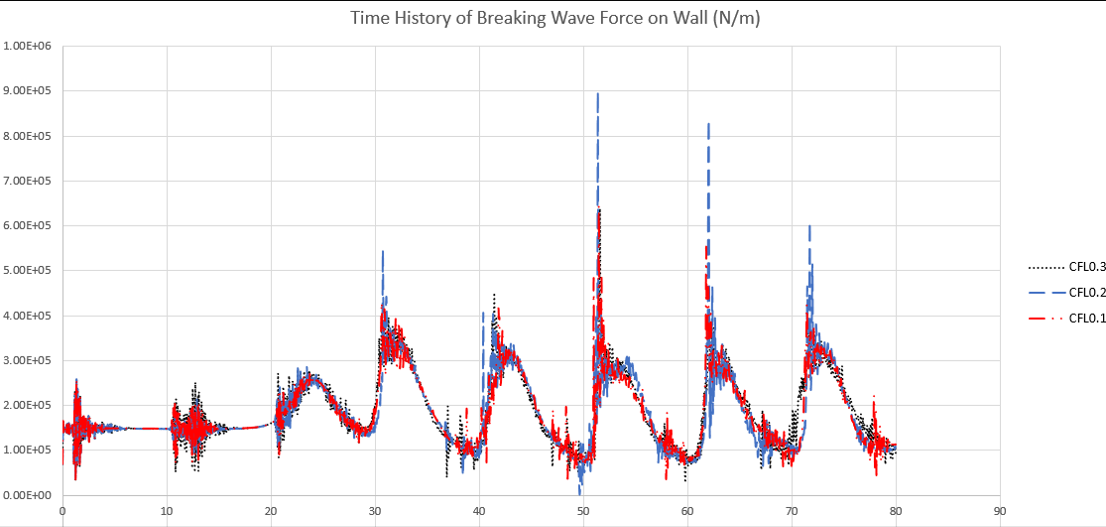
However, when it comes to breaking wave force, the result is quite sensitive to the CFL number. I get it since the accerleration value may be huge when wave interacts with DBC. From a stability point of view, since the free-surface elevation of all cases are similar and stable, I think all 3 choices of CFL number are fine. However, for accuracy, since I don't have a benchmark to compare to, I am not sure how to choose a better CFL number. Does it make sense to have smaller CFL number since this results in smaller dt?

Picture1.png

Thanks for your insight in advance!

Comments

  • Asalih3dAsalih3d

    Thanks for opening this post!

    I am a bit perplexed that the CFL number seems to have this influence in the second plot (I find in the first plot it is difficult to find any difference). It seems worrisome that the peak value of N/m can be influcenced this much by changing CFL, since "under the hood" DualSPHysics it self is analyzing what time step size to use for consistency.

    If possible could you share an animation of your case?

    Based on your post I also have a few follow up questions:

    1. Why do you get some noise at ~0 and ~10 seconds when the wall has not been touched yet? (Second plot)
    2. How did you extract N/m? To my knowledge DualSPHysics only allows extracting N - have you done some post-processing afterwards? Perhaps you could show the native force results too?

    Interesting findings.

    Kind regards

  • barrybarry

    Hi @Asalih3d .

    Thanks for your reply.

    Picture1.png

    A screenshot when the wave starts to break and move towards an inclined wall.

    For Q1:

    I think it comes from two reasons. First, DualSPHysics needs some time to converge even for hydrostatic case (only water pressure); second, the inlet(wavemaker) starts to work at t=0, so there are changes within the computational domain already. At t=10, although the crest of the wave hasn't touched the structure, there are movements already within the domain for the particles.

    For Q2:

    Since my case is just 2D, I think the result is N/m.

    Best

Sign In or Register to comment.

© Vanilla Keystone Theme 2024