Why can I not achieve consistency?
I am setting up an experiment to validate DualSPHysics's wave propagation, which I later want to use for a big WEC simulation.
I do however, have some problems in achieving any consistency.
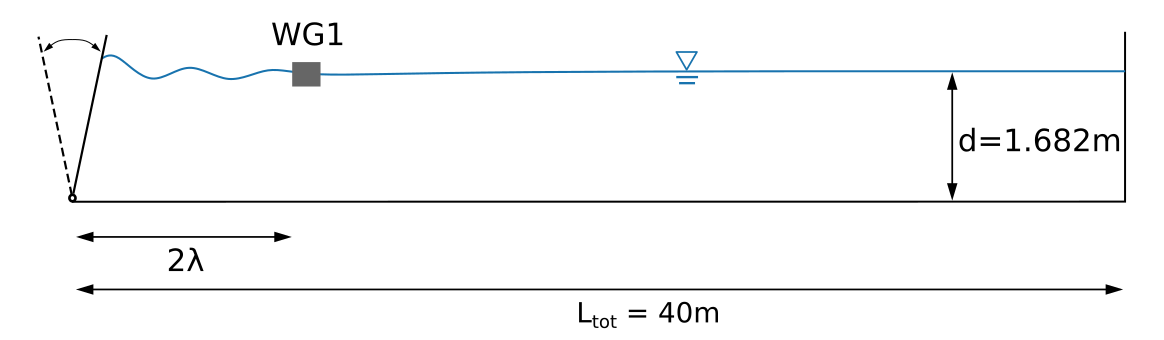
Setup is the following (2D):
- T = 1.42s
- λ = 3.14 m
- d = 1.682m
- H = 0.11m
- d/λ = 0.535 (deep water)
- H/λ = 0.035 (linear wave)
I now conducted 24 runs with different values of H/dp (5, 10, 15, 20, 25, 30) and different formulations of the viscosity term (SPS, α=0.01, α=0.001, α=0.0001).
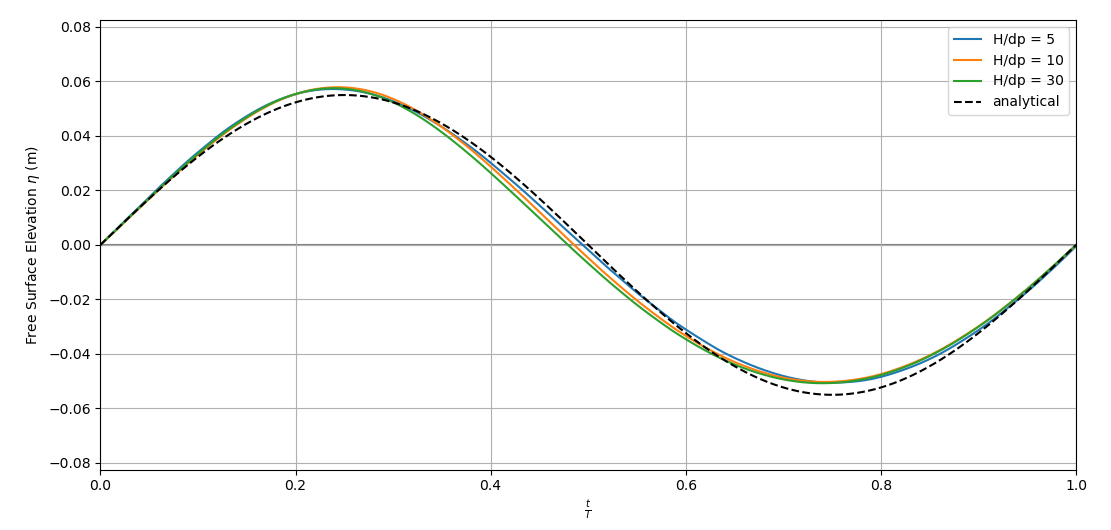
An example of a phase averaged period (by upcrossing analysis) is given in the following for SPS and 3 resolutions.
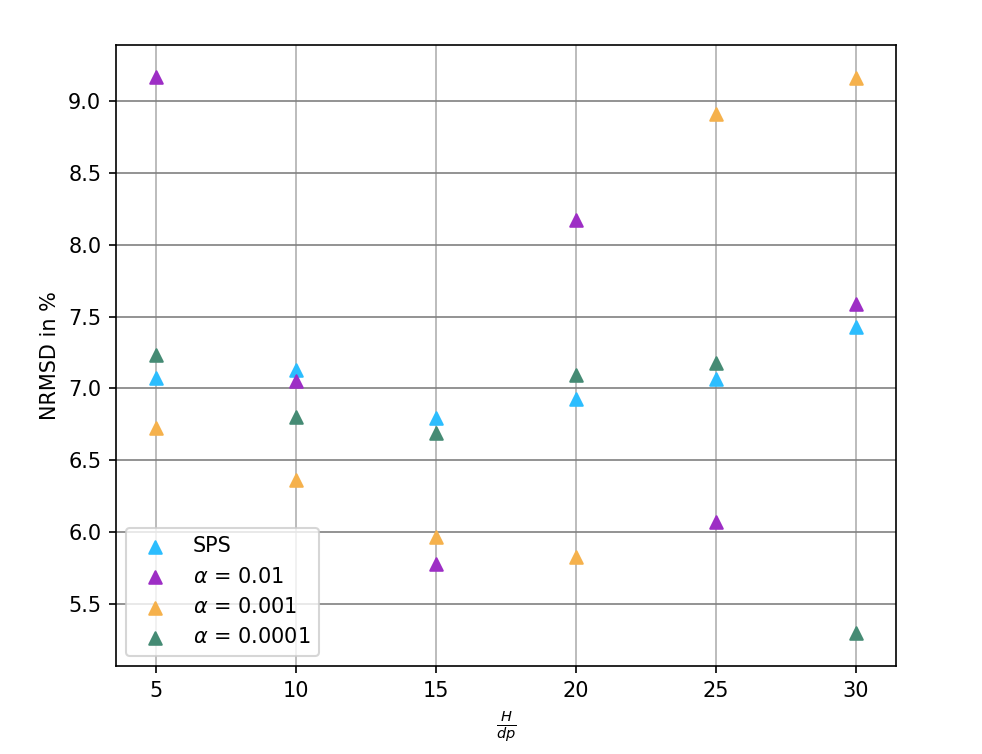
From the plot it is evident that the numerical solution is in fact diverging from the analytical one with increasing H/dp. Similar behaviour can be observed for the other viscosity formulations. To get an overview of all runs I calculated the "normalized (by H) root mean square deviation" (NRMSD) at WG1 and plotted it.
Again I am very confused by the fact that my numerical solution is not converging towards the analytical one with increasing spatial resolution. In fact it seems to perform worse for e.g. α=0.001 and SPS.
So I have two questions:
- Why can I not achieve consistency? Meaning numerical solution converges towards analytical one for better resolution.
- Why does my numerical wave seem to be shifted "up left" in comparison to the analytical one (see averaged period plot). I have been trying to figure this out for quite a while now but can't make any progress.
Example .xml file and Run output for SPS H/dp=5:
Debug Trace
| Notice |
rich is deprecated. Use FormatService::renderHtml($content, Formats\RichFormat::FORMAT_KEY) instead.
#0 [internal function]: gdn_ErrorHandler(16384, 'rich is depreca...', '/var/www/forums...', 950, Array)
#1 /var/www/forums-dual-sphysics-org/library/core/functions.general.php(950): trigger_error('rich is depreca...', 16384)
#2 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1729): deprecated('rich', 'FormatService::...')
#3 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"I a...')
#4 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(197): Gdn_Format::to('[{"insert":"I a...', 'Rich')
#5 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#6 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#7 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#8 {main} |
| Notice |
rich is deprecated. Use FormatService::renderHtml($content, Formats\RichFormat::FORMAT_KEY) instead.
#0 [internal function]: gdn_ErrorHandler(16384, 'rich is depreca...', '/var/www/forums...', 950, Array)
#1 /var/www/forums-dual-sphysics-org/library/core/functions.general.php(950): trigger_error('rich is depreca...', 16384)
#2 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1729): deprecated('rich', 'FormatService::...')
#3 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"I a...')
#4 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":"I a...', 'Rich')
#5 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/discussion.php(89): formatBody(Object(stdClass))
#6 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(31): include('/var/www/forums...')
#7 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#8 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#9 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#10 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#11 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#12 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#13 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#14 {main} |
| Notice |
rich is deprecated. Use FormatService::renderHtml($content, Formats\RichFormat::FORMAT_KEY) instead.
#0 [internal function]: gdn_ErrorHandler(16384, 'rich is depreca...', '/var/www/forums...', 950, Array)
#1 /var/www/forums-dual-sphysics-org/library/core/functions.general.php(950): trigger_error('rich is depreca...', 16384)
#2 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1729): deprecated('rich', 'FormatService::...')
#3 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"Dea...')
#4 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":"Dea...', 'Rich')
#5 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(170): formatBody(Object(stdClass))
#6 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/comments.php(19): writeComment(Object(stdClass), Object(DiscussionController), Object(Gdn_Session), 1)
#7 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(53): include('/var/www/forums...')
#8 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#9 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#10 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#11 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#12 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#13 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#14 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#15 {main} |
| Notice |
rich is deprecated. Use FormatService::renderHtml($content, Formats\RichFormat::FORMAT_KEY) instead.
#0 [internal function]: gdn_ErrorHandler(16384, 'rich is depreca...', '/var/www/forums...', 950, Array)
#1 /var/www/forums-dual-sphysics-org/library/core/functions.general.php(950): trigger_error('rich is depreca...', 16384)
#2 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1729): deprecated('rich', 'FormatService::...')
#3 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"You...')
#4 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":"You...', 'Rich')
#5 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(170): formatBody(Object(stdClass))
#6 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/comments.php(19): writeComment(Object(stdClass), Object(DiscussionController), Object(Gdn_Session), 2)
#7 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(53): include('/var/www/forums...')
#8 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#9 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#10 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#11 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#12 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#13 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#14 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#15 {main} |
| Notice |
Validation error while instantiating embed type image with class Vanilla\EmbeddedContent\Embeds\ImageEmbed and data
{
"embedType": "image",
"url": "https:\/\/forums.dual.sphysics.org\/uploads\/434\/1YOJVFEABVAW.png",
"name": "image.png",
"attributes": [],
"format": null,
"bodyRaw": null
}
{
"message": "Validation Failed",
"status": 400,
"errors": [
{
"field": "type",
"code": "missingField",
"status": 400,
"message": "type is required."
}
]
}
#0 [internal function]: gdn_ErrorHandler(512, 'Validation erro...', '/var/www/forums...', 217, Array)
#1 /var/www/forums-dual-sphysics-org/library/Vanilla/EmbeddedContent/EmbedService.php(217): trigger_error('Validation erro...', 512)
#2 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Blots/Embeds/ExternalBlot.php(78): Vanilla\EmbeddedContent\EmbedService->createEmbedFromData(Array)
#3 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Blots/Embeds/ExternalBlot.php(90): Vanilla\Formatting\Quill\Blots\Embeds\ExternalBlot->getEmbed()
#4 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/BlotGroup.php(170): Vanilla\Formatting\Quill\Blots\Embeds\ExternalBlot->render()
#5 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/BlotGroup.php(151): Vanilla\Formatting\Quill\BlotGroup->renderContent()
#6 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Renderer.php(25): Vanilla\Formatting\Quill\BlotGroup->render()
#7 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Formats/RichFormat.php(65): Vanilla\Formatting\Quill\Renderer->render(Object(Vanilla\Formatting\Quill\BlotGroupCollection))
#8 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/FormatService.php(34): Vanilla\Formatting\Formats\RichFormat->renderHTML('[{"insert":"You...')
#9 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1730): Vanilla\Formatting\FormatService->renderHTML('[{"insert":"You...', 'rich')
#10 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"You...')
#11 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":"You...', 'Rich')
#12 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(170): formatBody(Object(stdClass))
#13 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/comments.php(19): writeComment(Object(stdClass), Object(DiscussionController), Object(Gdn_Session), 2)
#14 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(53): include('/var/www/forums...')
#15 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#16 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#17 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#18 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#19 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#20 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#21 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#22 {main} |
| Notice |
Validation error while instantiating embed type image with class Vanilla\EmbeddedContent\Embeds\ImageEmbed and data
{
"embedType": "image",
"url": "https:\/\/forums.dual.sphysics.org\/uploads\/021\/X61V5W2E1LJH.png",
"name": "image.png",
"attributes": [],
"format": null,
"bodyRaw": null
}
{
"message": "Validation Failed",
"status": 400,
"errors": [
{
"field": "type",
"code": "missingField",
"status": 400,
"message": "type is required."
}
]
}
#0 [internal function]: gdn_ErrorHandler(512, 'Validation erro...', '/var/www/forums...', 217, Array)
#1 /var/www/forums-dual-sphysics-org/library/Vanilla/EmbeddedContent/EmbedService.php(217): trigger_error('Validation erro...', 512)
#2 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Blots/Embeds/ExternalBlot.php(78): Vanilla\EmbeddedContent\EmbedService->createEmbedFromData(Array)
#3 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Blots/Embeds/ExternalBlot.php(90): Vanilla\Formatting\Quill\Blots\Embeds\ExternalBlot->getEmbed()
#4 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/BlotGroup.php(170): Vanilla\Formatting\Quill\Blots\Embeds\ExternalBlot->render()
#5 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/BlotGroup.php(151): Vanilla\Formatting\Quill\BlotGroup->renderContent()
#6 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Quill/Renderer.php(25): Vanilla\Formatting\Quill\BlotGroup->render()
#7 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/Formats/RichFormat.php(65): Vanilla\Formatting\Quill\Renderer->render(Object(Vanilla\Formatting\Quill\BlotGroupCollection))
#8 /var/www/forums-dual-sphysics-org/library/Vanilla/Formatting/FormatService.php(34): Vanilla\Formatting\Formats\RichFormat->renderHTML('[{"insert":"You...')
#9 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1730): Vanilla\Formatting\FormatService->renderHTML('[{"insert":"You...', 'rich')
#10 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":"You...')
#11 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":"You...', 'Rich')
#12 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(170): formatBody(Object(stdClass))
#13 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/comments.php(19): writeComment(Object(stdClass), Object(DiscussionController), Object(Gdn_Session), 2)
#14 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(53): include('/var/www/forums...')
#15 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#16 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#17 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#18 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#19 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#20 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#21 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#22 {main} |
| Notice |
rich is deprecated. Use FormatService::renderHtml($content, Formats\RichFormat::FORMAT_KEY) instead.
#0 [internal function]: gdn_ErrorHandler(16384, 'rich is depreca...', '/var/www/forums...', 950, Array)
#1 /var/www/forums-dual-sphysics-org/library/core/functions.general.php(950): trigger_error('rich is depreca...', 16384)
#2 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1729): deprecated('rich', 'FormatService::...')
#3 /var/www/forums-dual-sphysics-org/library/core/class.format.php(1479): Gdn_Format::rich('[{"insert":{"em...')
#4 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(24): Gdn_Format::to('[{"insert":{"em...', 'Rich')
#5 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/helper_functions.php(170): formatBody(Object(stdClass))
#6 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/comments.php(19): writeComment(Object(stdClass), Object(DiscussionController), Object(Gdn_Session), 3)
#7 /var/www/forums-dual-sphysics-org/applications/vanilla/views/discussion/index.php(53): include('/var/www/forums...')
#8 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(778): include('/var/www/forums...')
#9 /var/www/forums-dual-sphysics-org/library/core/class.controller.php(1382): Gdn_Controller->fetchView('', false, false)
#10 /var/www/forums-dual-sphysics-org/library/core/class.pluggable.php(217): Gdn_Controller->xRender()
#11 /var/www/forums-dual-sphysics-org/applications/vanilla/controllers/class.discussioncontroller.php(310): Gdn_Pluggable->__call('render', Array)
#12 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(862): DiscussionController->index('2396', 'why-can-i-not-a...', '')
#13 /var/www/forums-dual-sphysics-org/library/core/class.dispatcher.php(279): Gdn_Dispatcher->dispatchController(Object(Gdn_Request), Array)
#14 /var/www/forums-dual-sphysics-org/index.php(29): Gdn_Dispatcher->dispatch()
#15 {main} |

Comments
Dear,
I see you are using 1st order generation and comparing with 1t order theoretical time series. Am I wrong?
I see that 2nd order prescribes a slightly sharper wave crest and differences also in the trough. If my understanding is correct, please use 2nd order generation.
Besides, so not use Laminar+SPS in 2D, since it's development was meant for 3D. I would rather recommend to use artificial viscosity with alpha=0.01. Rota Roselli et al. (2018) proved that alpha=0.01 was optimal value for wave propagation, together with H/dp=10.
You are right. I was generating linear first order waves. Checking Le Mehaute Diagram again, I found that I am actually in the second order domain:
That was a very silly mistake of mine, but sadly, after redoing the simulations with second order generation I am observing very similar results:
Again I am confused about the fact that my results are not getting better with increasing H/dp, and seem to be the best for H/dp=15. From my understanding this is what was defined as consistent behavior (error going down with better discretization). But I realized I had a mistake with terminology here:
Thus, my original question has to be adapted to "Why can I not achieve convergence?".
Adding up on this I read your suggestion about Roselli (2018) and found the following sentence: "However, convergence has not yet been completely proven in SPH and the choice of this parameter influences the contribution of artificial viscosity terms.". Also I read that there are consistency problems in SPH, due to the anti-symetry in the discretized kernel sampling (heterogeneously placed particles within the kernel support). Therefore, I assume I can not achieve convergence, because consistency is not fulfilled.
I again plotted the free surface elevation for some example H/dp. But I found that by the averaging procedure, which I used in the original question, I am in deed plotting without the phase error. So this time the plots are with phase error. The main error of the NRMSD plot from above therefore, seems to be coming from this phase shift.
alpha = 0.01
https://forums.dual.sphysics.org/uploads/434/1YOJVFEABVAW.pngSPS (which seems to be performing quite well also in 2D):
https://forums.dual.sphysics.org/uploads/021/X61V5W2E1LJH.pngSo my questions:
Sorry I forgot to quote. I am not sure if any notification is sent if I am not quoting.